Teorema Norton, Mudah!
Pada posting artikel sebelumnya, saya sudah membahas bagaimana analisa rangkaian menggunakan : Hukum kirchhoff & Teorema Thevenin. Pada artikel saat ini saya akan menjelaskan analisa rangkaian lainnya yaitu dengan menggunakan Teorema Norton. Untuk mengetahui gambaran tentang apa itu Teorema Norton, berikut saya kutipkan pernyataan dari sebuah sumber terpercaya : wikipedia.org tentang Teorema Norton tersebut, semoga kutipan dari sumber ini menjadi langkah awal bagi anda untuk mengetahui cara memahami Teorema Norton dengan mudah.
Dari kutipan diatas semoga anda mulai mendapatkan sedikit gambaran tentang Teorema Norton yang saya maksudkan. Selanjutnya untuk memahami lebih dalam lagi saya akan sertakan contoh rangkaian DC yang akan dianalisa dengan menggunakan teorema Norton ini. Sebelumnya saya sarankan untuk mengetahui terlebih dahulu tentang konsep analisa rangkaian menggunakan hukum kirchhoff dan Teorema Thevenin pada postingan saya sebelumnya :
- Mengenal dan memahami hukum kirchhoff dengan mudah dan
- Cara memahami Teorema Thevenin dengan mudah
karena contoh rangkaian yang akan dibahas adalah menggunakan rangkaian serta nilai besaran yang sama dengan artikel sebelumnya diatas dengan maksud agar anda bisa membandingkan antara penyelesaian analisa rangkaian menggunakan full hukum Kirchhoff dan atau Teorema Thevenin dibandingkan dengan analisa rangkaian menggunakan Teorema Norton sehingga anda bisa menyimpulkan penyelesaian mana yang lebih mudah, atau anda punya alternatif pembanding lain dalam menyelesaikan analisa suatu rangkaian sehingga bisa lebih yakin kebenarannya.
Dari gambar rangkaian diatas, tentukan besarnya arus I1, I2, I3 ?
Solusi :
Tentukan prediksi arah mengalirnya arus I1, I2, I3 kemudian lepas resistor beban R3 untuk mendapatkan sumber Arus Norton ( Ino ) dan Resistansi Norton ( Rno )
Dari rangkaian diatas, I hubung singkat ( I norton ) = I yang melalui R1 + I yang melalui R2
Ino = V1/R1 + V2/R2
= (6V/ 10 Ohm) + (9V/20 Ohm)
Ino = 1,05 Ampere
Rno = R1 // R2
= (10 Ohm * 20 Ohm) / (10 Ohm + 20 Ohm )
Rno = 6,67 Ohm
Setelah Ino dan Rno diketahui, maka bisa dibuat rangkaian ekuivalen norton sebagai berikut :
Dari ragkaian ekuivalen Norton diatas kita bisa menghitung tegangan V total yaitu tegangan V di Rno = V di R3 yaitu dengan cara :
Hitung R total rangkaian ekuivalen tersebut : Rno // R3
R total = (6,67 Ohm * 30 Ohm ) / (6,67 Ohm + 30 Ohm )
R total = 5,4568 Ohm
Sehingga, V total = Rtotal * I Norton
V total = 5,4568 Ohm * 1,05 Amper
V total = 5,7296 Volt
Sampai langkah ini, kita sudah bisa menemukan besarnya arus yang mengalir di R3 yaitu I3 sesuai yang diminta pertanyaan soal.
I3 = V total / R3
I3 = 5,7296 Volt / 30 Ohm
I3 = 0,1909 Ampere
Setelah I3 ditemukan, mari kita kembali lagi ke rangkaian awal :
Mari kita gunakan hukum Kirchhoff KVL untuk rangkaian diatas :
Loop 1 :
I1 ( R1 ) +I3 ( R3 ) - V1 = 0
I1 ( 10 Ohm ) + 0,1909 A ( 30 Ohm ) - 6 V = 0
I1 = 0,273 V / 10 Ohm
I1= 0,0273 Ampere
Loop 2 :
I2 ( R2 ) +I3 ( R3 ) - V2 = 0
I2 ( 20 Ohm ) + 0,1909 A ( 30 Ohm ) - 9 V = 0
I2 = 3,273 V / 20 Ohm
I2 = 0,1636 Ampere
Atau untuk pencarian arus terakhir, I1 atau I2 bisa juga mengguakan kirchoff arus ( KCL ) terserah anda, hasil perhitungan akan sama jika prosesnya benar.
I1 + I2 - I3 = 0 ( silahkan diproses sendiri, hasilnya akan sama seperti diatas ....:))
Jadi, dengan menggunakan Teorema Norton sama halnya seperti menggunakan Teorema Thevenin, anda akan mendapatkan rangkaian ekuivalen yang lebih sederhana untuk dianalisa dan nilai arus I1, I2 dan I3 yang didapat ternyata besarnya sama persis dengan metode analisa rangkaian yang menggunakan hukum kirchhoff dengan banyak loop arus serta persamaan matematis yang harus dieliminasi dan di substitusi. Silahkan cek kembali proses perhitungan antara Hukum kirchhoff , Teorema Thevenin di artikel saya sebelumnya, bandingkan dengan proses perhitungan menggunakan Teorema Norton diatas.
Mana yang lebih mudah menurut anda... :)
Demikianlah artikel singkat tentang cara memahami Teorema Norton dengan mudah. Saran, masukan ataupun koreksi silahkan meninggalkan jejak di kolom komentar.
Pengertian Teorema Norton
Teorema Norton adalah salah satu teorema yang berguna untuk analisis sirkuit listrik.[1] Teorema Norton menunjukkan bahwa keseluruhan jaringan listrik tertentu, kecuali beban, dapat diganti dengan sirkuit ekuivalen yang hanya mengandung sumber arus listrik independen dengan sebuah resistor yang terhubung secara paralel, sedemikian hingga hubungan antara arus listrik dan tegangan pada beban tidak berubah.[1] Sirkuit baru hasil dari aplikasi teorema Norton disebut dengan sirkuit ekuivalen Norton.[1] Teorema ini dinamakan sesuai dengan penemunya, seorang insinyur yang pernah bekerja pada Bell Telephone Laboratories, yang bernama E. L. Norton[1]
Ditentukan sebuah jaringan listrik seperti pada gambar dan bagian dalam kotak hitam yang akan dicari sirkuit ekuivalennya; nilai sumber arus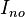 pada sirkuit ekuivalen Norton didapatkan dengan membuat hubungan-singkat antara terminal A dan B lalu dihitung besar arus yang mengalir melalui terminal tersebut.[2] Sedangkan nilai resistor pengganti
pada sirkuit ekuivalen Norton didapatkan dengan membuat hubungan-singkat antara terminal A dan B lalu dihitung besar arus yang mengalir melalui terminal tersebut.[2] Sedangkan nilai resistor pengganti  dapat dihitung dengan mematikan semua sumber tegangan dan arus lalu dihitung nilai ekuivalen resistansi di antara terminal A dan B.[2]
dapat dihitung dengan mematikan semua sumber tegangan dan arus lalu dihitung nilai ekuivalen resistansi di antara terminal A dan B.[2]
Penggunaan utama dari teorema Norton adalah menyederhanakan sebagian besar dari sirkuit dengan sirkuit ekuivalen yang sederhana.[3]
Keterangan Referensi :
[1] ^ a b c d (Inggris)Irwin, J. David; Kerns, David V., Jr. Introduction to Electrical Engineering (dalam Inggris) (1 ed.). Prentice Hall. p. 70-77. ISBN 978-0023599309.
[2] ^ a b (Inggris)"Norton's Theorem". AllAboutCircuits.com.
[3] ^ (Inggris)Hayt, William Hart; Kemmerly, Jack; Durbin, Steven (2007). Engineering Circuit Analysis (dalam Inggris) (7th ed.). McGraw-Hill Higher Education. p. 139-149. ISBN 978-0-07286611-7.
 |
| Ilustrasi sirkuit equivalen Norton |
Ditentukan sebuah jaringan listrik seperti pada gambar dan bagian dalam kotak hitam yang akan dicari sirkuit ekuivalennya; nilai sumber arus
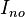 pada sirkuit ekuivalen Norton didapatkan dengan membuat hubungan-singkat antara terminal A dan B lalu dihitung besar arus yang mengalir melalui terminal tersebut.[2] Sedangkan nilai resistor pengganti
pada sirkuit ekuivalen Norton didapatkan dengan membuat hubungan-singkat antara terminal A dan B lalu dihitung besar arus yang mengalir melalui terminal tersebut.[2] Sedangkan nilai resistor pengganti  dapat dihitung dengan mematikan semua sumber tegangan dan arus lalu dihitung nilai ekuivalen resistansi di antara terminal A dan B.[2]
dapat dihitung dengan mematikan semua sumber tegangan dan arus lalu dihitung nilai ekuivalen resistansi di antara terminal A dan B.[2]Penggunaan utama dari teorema Norton adalah menyederhanakan sebagian besar dari sirkuit dengan sirkuit ekuivalen yang sederhana.[3]
Keterangan Referensi :
[1] ^ a b c d (Inggris)Irwin, J. David; Kerns, David V., Jr. Introduction to Electrical Engineering (dalam Inggris) (1 ed.). Prentice Hall. p. 70-77. ISBN 978-0023599309.
[2] ^ a b (Inggris)"Norton's Theorem". AllAboutCircuits.com.
[3] ^ (Inggris)Hayt, William Hart; Kemmerly, Jack; Durbin, Steven (2007). Engineering Circuit Analysis (dalam Inggris) (7th ed.). McGraw-Hill Higher Education. p. 139-149. ISBN 978-0-07286611-7.
Dari kutipan diatas semoga anda mulai mendapatkan sedikit gambaran tentang Teorema Norton yang saya maksudkan. Selanjutnya untuk memahami lebih dalam lagi saya akan sertakan contoh rangkaian DC yang akan dianalisa dengan menggunakan teorema Norton ini. Sebelumnya saya sarankan untuk mengetahui terlebih dahulu tentang konsep analisa rangkaian menggunakan hukum kirchhoff dan Teorema Thevenin pada postingan saya sebelumnya :
- Mengenal dan memahami hukum kirchhoff dengan mudah dan
- Cara memahami Teorema Thevenin dengan mudah
Contoh Soal Rangkaian Teorema Norton
karena contoh rangkaian yang akan dibahas adalah menggunakan rangkaian serta nilai besaran yang sama dengan artikel sebelumnya diatas dengan maksud agar anda bisa membandingkan antara penyelesaian analisa rangkaian menggunakan full hukum Kirchhoff dan atau Teorema Thevenin dibandingkan dengan analisa rangkaian menggunakan Teorema Norton sehingga anda bisa menyimpulkan penyelesaian mana yang lebih mudah, atau anda punya alternatif pembanding lain dalam menyelesaikan analisa suatu rangkaian sehingga bisa lebih yakin kebenarannya.
 |
| Contoh Soal Teorema Norton |
Dari gambar rangkaian diatas, tentukan besarnya arus I1, I2, I3 ?
Solusi :
Tentukan prediksi arah mengalirnya arus I1, I2, I3 kemudian lepas resistor beban R3 untuk mendapatkan sumber Arus Norton ( Ino ) dan Resistansi Norton ( Rno )
 |
| Penentuan prediksi arah arus I1, I2, I3 |
Menghitung I Norton (Ino)
nilai sumber
arus 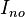 pada sirkuit ekuivalen Norton didapatkan dengan membuat
hubungan-singkat antara terminal A dan B lalu dihitung besar arus yang
mengalir melalui terminal tersebut
pada sirkuit ekuivalen Norton didapatkan dengan membuat
hubungan-singkat antara terminal A dan B lalu dihitung besar arus yang
mengalir melalui terminal tersebut
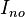 pada sirkuit ekuivalen Norton didapatkan dengan membuat
hubungan-singkat antara terminal A dan B lalu dihitung besar arus yang
mengalir melalui terminal tersebut
pada sirkuit ekuivalen Norton didapatkan dengan membuat
hubungan-singkat antara terminal A dan B lalu dihitung besar arus yang
mengalir melalui terminal tersebut |
| Rangkaian menentukan sumber arus Ino |
Dari rangkaian diatas, I hubung singkat ( I norton ) = I yang melalui R1 + I yang melalui R2
Ino = V1/R1 + V2/R2
= (6V/ 10 Ohm) + (9V/20 Ohm)
Ino = 1,05 Ampere
Menghitung R Norton (Rno)
Nilai resistor pengganti  dapat dihitung dengan mematikan semua sumber tegangan dan arus lalu
dihitung nilai ekuivalen resistansi di antara terminal A dan B
dapat dihitung dengan mematikan semua sumber tegangan dan arus lalu
dihitung nilai ekuivalen resistansi di antara terminal A dan B
 dapat dihitung dengan mematikan semua sumber tegangan dan arus lalu
dihitung nilai ekuivalen resistansi di antara terminal A dan B
dapat dihitung dengan mematikan semua sumber tegangan dan arus lalu
dihitung nilai ekuivalen resistansi di antara terminal A dan B |
| Rangkaian menentukan tahanan pengganti norton Rno |
Rno = R1 // R2
= (10 Ohm * 20 Ohm) / (10 Ohm + 20 Ohm )
Rno = 6,67 Ohm
Rangkaian Ekuivalen Norton
Setelah Ino dan Rno diketahui, maka bisa dibuat rangkaian ekuivalen norton sebagai berikut :
 |
| Rangkaian ekuivalen Norton |
Dari ragkaian ekuivalen Norton diatas kita bisa menghitung tegangan V total yaitu tegangan V di Rno = V di R3 yaitu dengan cara :
Hitung R total rangkaian ekuivalen tersebut : Rno // R3
R total = (6,67 Ohm * 30 Ohm ) / (6,67 Ohm + 30 Ohm )
R total = 5,4568 Ohm
Sehingga, V total = Rtotal * I Norton
V total = 5,4568 Ohm * 1,05 Amper
V total = 5,7296 Volt
Sampai langkah ini, kita sudah bisa menemukan besarnya arus yang mengalir di R3 yaitu I3 sesuai yang diminta pertanyaan soal.
I3 = V total / R3
I3 = 5,7296 Volt / 30 Ohm
I3 = 0,1909 Ampere
Setelah I3 ditemukan, mari kita kembali lagi ke rangkaian awal :
 |
| Rangkaian untuk mencari I1 dan I2 |
Mari kita gunakan hukum Kirchhoff KVL untuk rangkaian diatas :
" Jumlah aljabar dari semua tegangan dalam sebuah loop tertutup sama dengan nol "
Loop 1 :
I1 ( R1 ) +I3 ( R3 ) - V1 = 0
I1 ( 10 Ohm ) + 0,1909 A ( 30 Ohm ) - 6 V = 0
I1 = 0,273 V / 10 Ohm
I1= 0,0273 Ampere
Loop 2 :
I2 ( R2 ) +I3 ( R3 ) - V2 = 0
I2 ( 20 Ohm ) + 0,1909 A ( 30 Ohm ) - 9 V = 0
I2 = 3,273 V / 20 Ohm
I2 = 0,1636 Ampere
Atau untuk pencarian arus terakhir, I1 atau I2 bisa juga mengguakan kirchoff arus ( KCL ) terserah anda, hasil perhitungan akan sama jika prosesnya benar.
" jumlah aljabar semua arus pada titik percabangan sama dengan nol "
I1 + I2 - I3 = 0 ( silahkan diproses sendiri, hasilnya akan sama seperti diatas ....:))
Jadi, dengan menggunakan Teorema Norton sama halnya seperti menggunakan Teorema Thevenin, anda akan mendapatkan rangkaian ekuivalen yang lebih sederhana untuk dianalisa dan nilai arus I1, I2 dan I3 yang didapat ternyata besarnya sama persis dengan metode analisa rangkaian yang menggunakan hukum kirchhoff dengan banyak loop arus serta persamaan matematis yang harus dieliminasi dan di substitusi. Silahkan cek kembali proses perhitungan antara Hukum kirchhoff , Teorema Thevenin di artikel saya sebelumnya, bandingkan dengan proses perhitungan menggunakan Teorema Norton diatas.
Mana yang lebih mudah menurut anda... :)
Demikianlah artikel singkat tentang cara memahami Teorema Norton dengan mudah. Saran, masukan ataupun koreksi silahkan meninggalkan jejak di kolom komentar.
Wassalam.
6 komentar untuk "Teorema Norton, Mudah!"
mohon pencerahannya
terimakasih koreksi dan masukannya, semoga menjadi amal jariyah untuk agan.
bukannya harusnya Ampere ya?
Silahkan berkomentar yang sesuai dengan topik, Mohon Maaf komentar dengan nama komentator dan isi komentar yang berbau P*RN*GRAFI, OB*T, H*CK, J*DI dan komentar yang mengandung link aktif, Tidak akan ditampilkan!